Played Result


| Record |
Maths  |
Played Result


| Record |
Maths  |
Both hands give the same result so
| Record |
Maths  |
By not showing what x was declared as we can form a puzzle to find the declared value of x
When we solved
| Record |
Maths  |
in The Multiplication Puzzle we took 3x as the played hand and 21 as the result on the board.
Doing the same with 5x + 2 = 3x + 8 we would take 5x + 2 as the played hand
and 3x + 8 as the result on the board.
What does an x piece played on the board look like?
In this case x is declared as 3, so take three black counters and hide them in a box and label the box with an x



Counters in box Close box Label box
Now as the wildbox,
 , contains three black counters make a negative wildbox that contains three white counters,
, contains three black counters make a negative wildbox that contains three white counters,  .
. Removing the counters gives three pairs of

 in other words Zero.
in other words Zero.So the pair

 is another form of Zero and can be removed.
is another form of Zero and can be removed.TIP In solving this type of puzzle always play cards that will remove wildboxes from the board.
We set up the board by playing a wildbox,
 , for the wildcard
, for the wildcard 
Having put three black counters in the wildbox this declares the wildcard as a Three.
Set the Puzzle
Played Result

Swap the hand for the other one that gives the same result which gives the puzzle to play
Puzzle


Played Result













| Record |
Maths  |




 cut it into card sized holders
cut it into card sized holders 




 or
or 
 or
or  which is
which is 





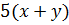
 and
and  however we know that
however we know that  what those values are.
what those values are. and
and  and we have factorised the number
and we have factorised the number