What, for example, would be the result of
 ?
?This is
 and from New Numbers, Old Rules this is the same as
and from New Numbers, Old Rules this is the same as 
Let’s go back to using boxes and apples.
 is 1 ÷ 5 , that is, one apple divided over five boxes and
is 1 ÷ 5 , that is, one apple divided over five boxes and  is the result of 1 ÷ 5 divided over
is the result of 1 ÷ 5 divided overfour boxes.
We can do this by using five gift boxes each holding four boxes





Share the apple over the five gift boxes and then the one fifths of the apple over the four boxes.
What we have then done is share the apple over five times four or twenty boxes.
The result of 1/5×1/4= 1/20
A more general example would be

What is
 ? We know
? We know  and
and 
So

and because order of multiplication does not matter

The numerator, 6, is found by multiplying the numerators 2 and 3.
The denominator, 20, is found by multiplying the denominators 5 and 4.
We have not quite finished yet as we see that 6 and 20 have a highest common factor of 2 and to make the numerator and denominators of fractions as small as possible cancel by the HCF.

If we look earlier we can see that 2 and 4 have the factor 2 in common so we could do some cancelling before we do any multiplication.

It is always worth checking out to see if any of the numbers in the numerators have any common factors with the numbers in the denominators. Cancelling such factors makes the multiplication numbers much smaller.
The Game of Maths

Remember that numerators are the number of counters and the denominators are the number of boards. Change to a many boards hand matching the numerator in the holder to a holder for the counters card and the denominator in the holder to a holder for the boards card.
Do the multiplications, look for common factors and cancel.

All the above give the same result.
A Further Example
The Game of Maths

Gives the same result as the following


In the record it is probably easier to see how to cancel factors earlier.
Looking at the record you need to remember that 1 is always a factor of any number and that 4 x 3 x 5 = 4 x 3 x 5 x 1 and so cancelling 4, 3 and 5 still leaves 1 as the result.
| Record |
Maths   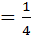 |
Sometimes you can do the cancelling even earlier and show it like this

We see that 5 is a factor of 5 in the numerator and 15 in the denominator.
Now 5 = 5 x 1 and 15 = 5 x 3 and so cancel the 5, giving a 1 in the numerator and 3 in the denominator.
We see that 4 is a factor of 12 in the numerator and 16 in the denominator.
Now 12 = 4 x 3 and 16 = 4 x 4 and so cancel the 4, giving a 3 in the numerator and a 4 in the denominator.
We now see that there is a 3 = 3 x 1 in the numerator and the denominator so cancel the 3 giving a 1 in the numerator and the denominator.
No comments:
Post a Comment